To start this assignment, download this zip file.
Extra Bit problems
1. Green bucket
Bit starts in a 7x5 world:
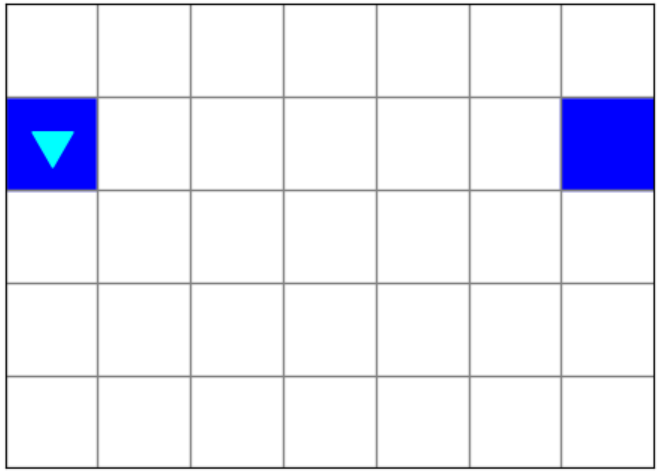
Bit should paint the edges of a bucket:
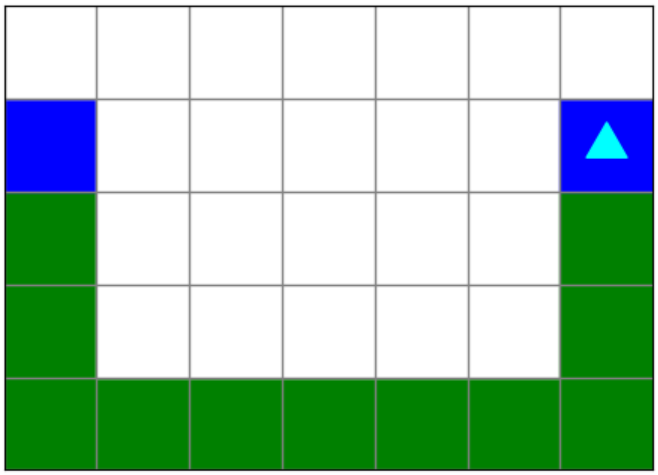
In the code we have given you, we have decomposed the problem for you:
from byubit import Bit
# Will paint green until bit is blocked
def go_green(bit):
pass
# Will paint green until bit reaches a blue square
def paint_green_until_blue(bit):
pass
@Bit.worlds('green-bucket', 'another-green-bucket')
def make_bucket(bit):
pass
if __name__ == "__main__":
make_bucket(Bit.new_bit)2. Roofing
Bit is roofing in a 17x5 world and a 22x5 world.
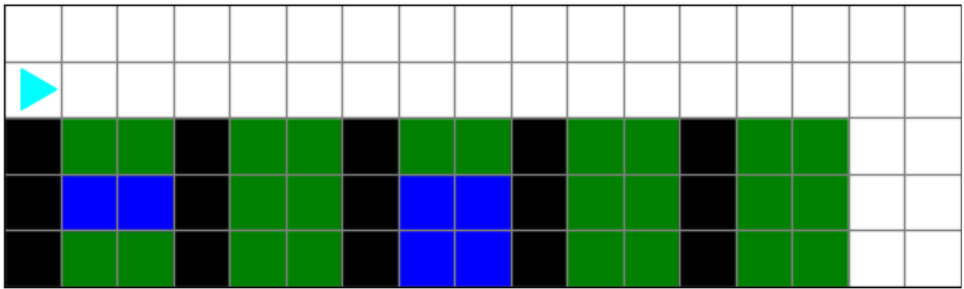
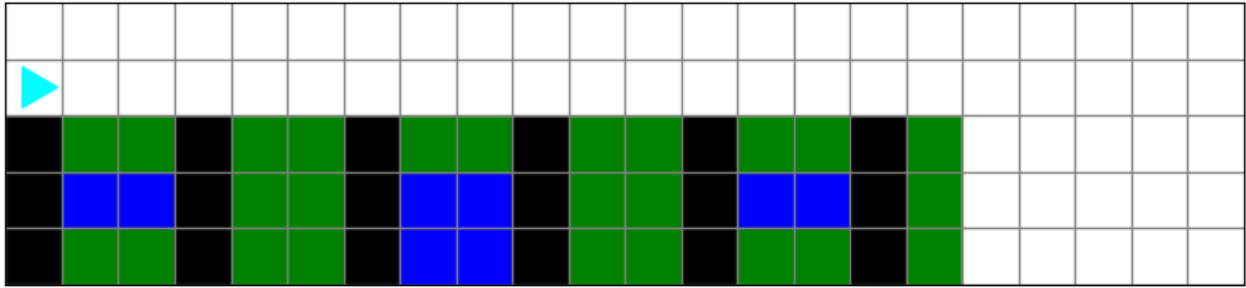
Bit should roof both houses:
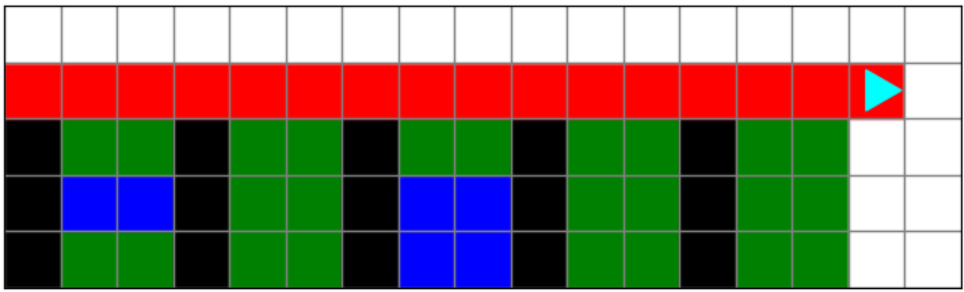
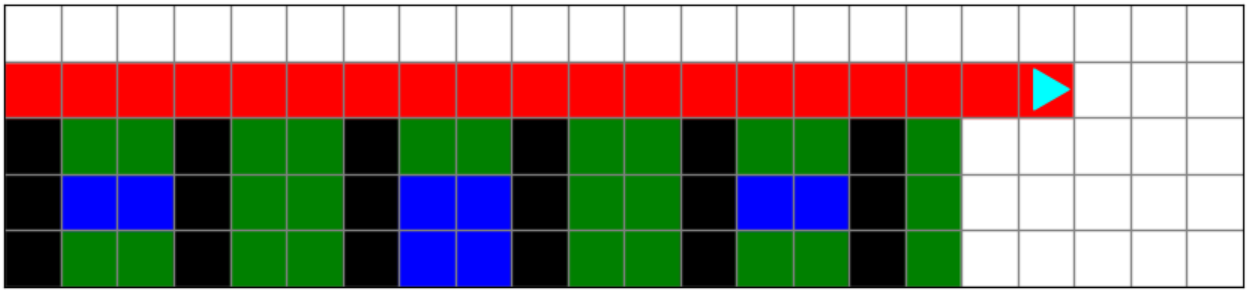
In the code we have given you, we have decomposed the problem for you:
from byubit import Bit
# Will paint red until bit is blocked on the right again
def paint_green_until_blue(bit):
pass
@Bit.worlds('roofing', 'more-roofing')
def go(bit):
pass
if __name__ == "__main__":
go(Bit.new_bit)3. Red square
Bit is painting a 2x2 red square in a 3x3 world.
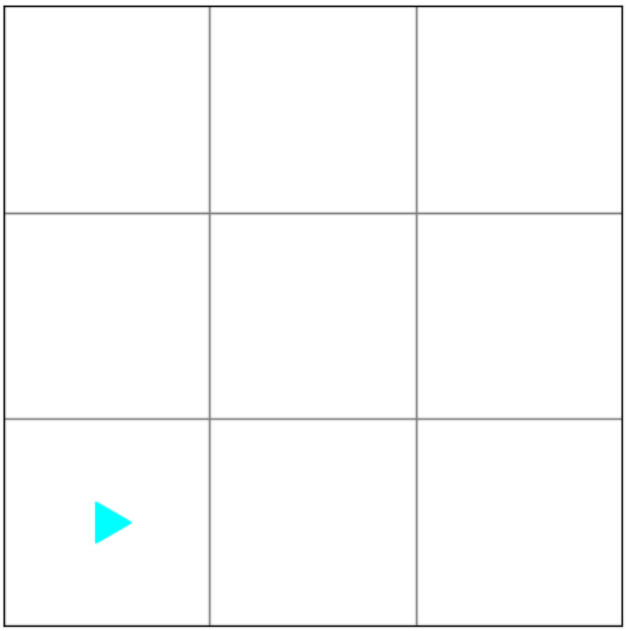
The resulting world should look like this:
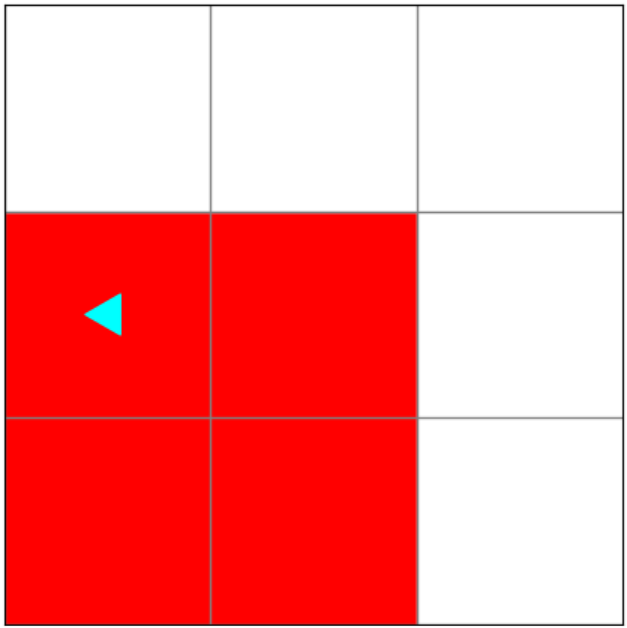
The starting file looks like this:
from byubit import Bit
@Bit.empty_world(3, 3)
def go(bit):
pass
if __name__ == "__main__":
go(Bit.new_bit)4. Blue to green
Bit starts on the right side of a 7x3 world.
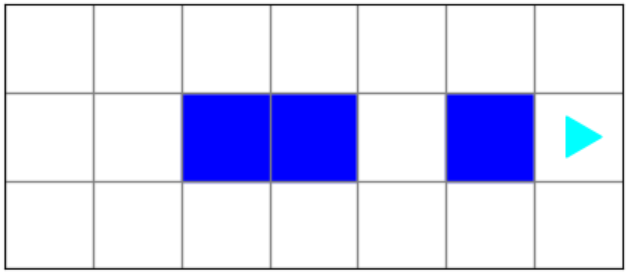
Bit should end on the left side and turn all blue squares into green squares:
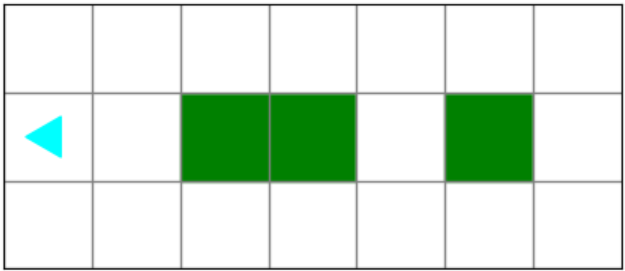
The starting file looks like this:
from byubit import Bit
@Bit.worlds('blue-to-green')
def do_stuff(bit):
pass
if __name__ == "__main__":
do_stuff(Bit.new_bit)5. Diagonals
Bit begins in an empty 10 x 10 world. It should paint until it reaches the bottom-right hand corner. It also needs to cycle through colors (red, blue, and green) such that the colors of the diagonals alternate.
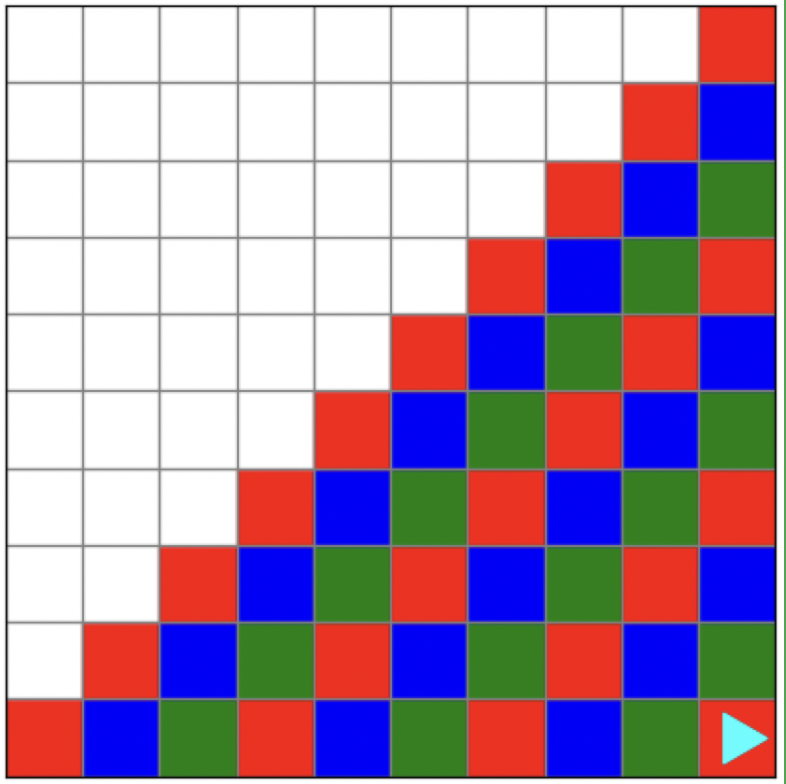
How could we make bit cycle through colors? Well, if we stored possible colors in a list, we can develop some logic to cycle through them.
colors = ['red', 'blue', 'green']Using a count variable and modular arithmetic, we can index into the list with 0, 1, 2. In this case,
colors[0] = 'red'
colors[1] = 'blue'
colors[2] = 'green'To cycle through 0, 1, 2, we will use the modulo 3 operator with a count variable to keep track of what iteration we are on. To illustrate how this works, let’s walk through a few of the iterations.For the first diagonal, our count will be set to 0.
0 % 3 = 0
1 % 3 = 1
2 % 3 = 2
3 % 3 = 0
4 % 3 = 1and so on.
For the count , we need to increment it (count += 1) so that it updates after each iteration. After the first iteration, the count should be set to 1.
1 % 3 = 1 and colors[1] is ‘blue’. Continuing the pattern, the 3rd iteration and 4th iterations will be as follows: 3rd. Count = 2, 2 % 3 = 2, and colors[2] = ‘green’. 4th. Count = 3, 3 % 3 = 0, and colors[0] = ‘red’.
The cycle continues. Here is a possible way to format the code:
colors = ['red', 'blue', 'green']
count = 0
while _____:
color = colors[count % 3]
count += 1